algorithm

4. 알고리즘의 시간 복잡도 분석

알고리즘 문제 해결 전략을 읽고 요약했습니다.

4. 알고리즘의 시간 복잡도 분석

4.1 도입

알고리즘의 속도는 어떻게 측정할 수 있을까?

프로그램을 구현한 뒤 같은 입력에 대해 프로그래밍의 수행시간을 비교

-> 부적합

  1. 사용 프로그래밍 언엉, 하드웨어, 운영체제, 컴파일러등 수 많은 요소에 의해 변할 수 있음
  2. 프로그램의 실제 수행 시간이 다양한 입력에 대한 실험 시간을 반영하지 못함
    • 입력의 크기나 특성에 따라 수행 시간이 달라질 수 있다.

반복문이 지배한다

  • 지배한다 (Dominate)
    • 한가지 항목이 전체의 대소를 좌지우지 하는 것
  • 알고리즘의 시간을 지배하는 것 -> “반복문”
    • 입력의 크기가 작을 때는 반복 외의 다른 부분들이 갖는 비중이 클 수 있지만, 입력의 크기가 커지면 커질수록 반복문이 알고리즘의 수행시간을 지배한다.
    • 반복문의 수행 횟수는 입력의 크기에 대한 함수로 표현
  • eg) 주어진 배열에서 가장 많이 등장하는 숫자를 반환하기
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

    def majority_1(A):
    n = len(A)
    majority = -1
    majority_count = 0
    for i in A:
        count = 0
        for j in A:
            if j == i:
                count += 1
        if count > majority_count:
            majority_count = count
            majority = i
    return majority

    • 알고리즘의 수행시간은 입력 크기 N에 따라 변한다.

    • N 번 수행되는 반복문이 두 개 겹쳐 있으므로, 반복문의 가장 안쪽은 항상 $N^2$번 실행

      -> 알고리즘의 수행시간은 $N^2$

  • if 입력으로 주어지는 숫자들이 100점 만점의 수학 점수
     1
 2
 3
 4
 5
 6
 7
 8
 9
10

    def majority_2(A):
    n = len(A)
    count = [0] * 101
    for i in A:
        count[i] += 1
    majority = 0
    for i in range(1, 101):
        if count[i] > count[majority]:
            majority = i
    return majority

    • 하나는 N번, 하나는 100번

      -> 전체 반복문 수행 횟수 N + 100

    • N이 커질수록 후자의 방복문의 비중은 감소한다.

      -> 알고리즘 수행시간: $N$

4.2 선형 시간 알고리듬

다이어트 현황 파악: 이동 평균 계산하기

  • 이동 평균(Moving Average)
    • 시간에 따라 변화하는 값들을 관찰할 때 유용하게 사용할 수 있는 통계적 기준
  • eg) $N$개의 측정치가 주어질 때, M 간의 이동평균 계산
    1
2
3
4
5
6
7
8
9

    def moving_average(A, M):
    ret = []
    N = len(A)
    for i in range(M-1, N):
        partial_sum = 0
        for j in range(M):
            partial_sum += A[i-j]
        ret.append(partial_sum / M)
    return ret

    • 2개의 for loop

      1. $j$를 사용하는 반복문: $N$
      2. $i$를 사용하는 반복문: $N-M+1$

      -> $N * (N-M+1)=N^2-NM+N$

    • 중복된 계산을 없애기

      • $M-1$일과 $M$일을 비교
      • 0과 M일만 차이나고 모두 동일하다
      • $M-1$일에서 구한 몸무게 합에서 0일을 버리고 M일을 더하면?
         1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

        def moving_average(A, M):
    ret = []
    N = len(A)
    partial_sum = 0
    for i in range(M-1, N):
        parital_sum += A[i]
    for j in range(M):
        partial_sum += A[i]
        ret.append(partial_sum / M)
        partial_sum -= A[i-M+1]
    return ret
        • 하나로 묶여 있던 두 개의 반복문이 분리
          -> $M-1 +(N-M+1) = N$
        • 코드의 수행시간은 $N$에 정비례

          • N이 2배가 되면 실행도 2배 걸리고, 반으로 줄어들면 수행시간도 반으로 줄어든다.

          • 입력의 크기에 대비해 걸리는 시간을 그래프로 그러벼몬 정확히 직선이다

            -> 선형 시간(Linear Time) 알고리즘

4.3 선형 이하 시간 알고리듬

  • 어떤 문제건 입력된 자료를 모두 한 번 훑어 보는 데에는 입력의 크기에 비례하는 시간, 즉 선형시간이 걸린다.
  • 선형 시간보다 빠르게 동작하는 알고리즘은 입력된 값도 다 보지 않는다는 뜻.
    • 입력으로 주어진 자료에 대해 우리가 알고 있는 지식을 활용하면 가능하다!

이진 탐색

  • $binsearch(A[],x)$
  • 오름차순으로 정려된 $A[]$와 찾고 싶은 값 $x$가 주어질 때
    • $A[i-1] < x \le A[i]$인 $i$를 반환
    • 이 때 $A[-1] = - \infty, A[N] = \infty$로 가정한다.
    • 배열 $A[]$에서 $x$를 삽입할 수 있는 위치 중 가장 앞에 있는 것을 반환한다.

4.4 지수 시간 알고리듬

다항시간 알고리듬

  • 반복문의 수행 횟수를 입력 크기의 다항식으로 표현할 수 있는 알고리즘
  • eg) 알러지가 심한 친구들
    • 집들이에 $N$명의 친구를 초대 / 할 줄 아는 $M$가지 음식 중 무엇을 대접해야 할까? img
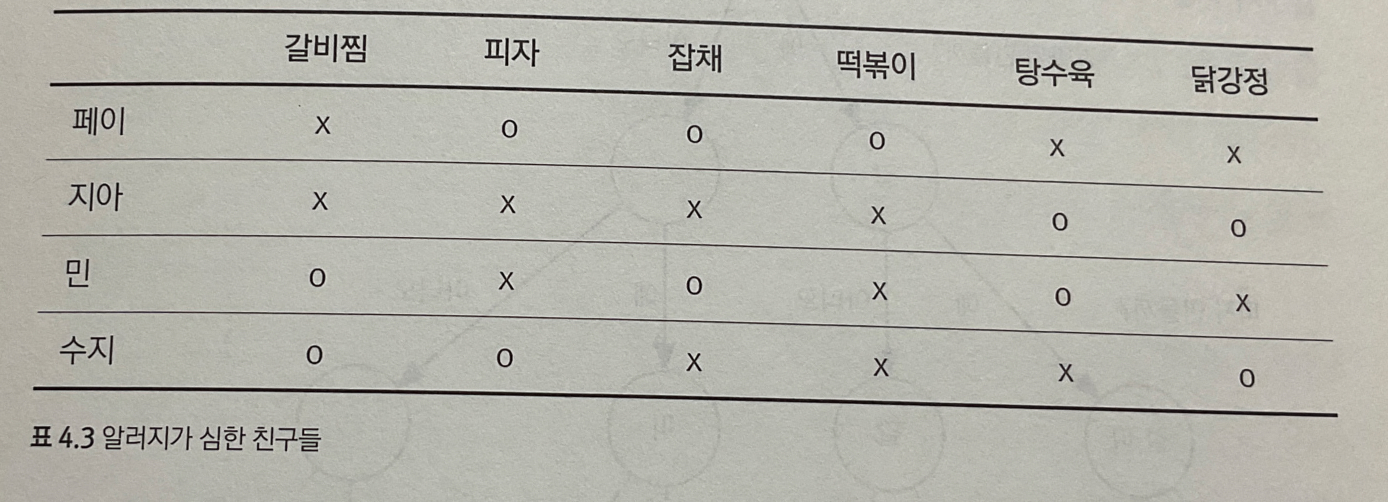
    • 모든 답 후보 평가하기
      • 이 문제는 여러 개의 답이 있을 수 있다.
      • 만들 수 있는 모든 음식을 다 만들면 된다 -> 더 적은 종류의 음식만을 준비하고 싶다.
      • 여러개의 답이 있고 그 중 가장 좋은 답을 찾을 때, 가장 간단한 방법은 모든 답을 일일이 고려해 보는 것 img
       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

      INF = 987654321
def can_everybody_eat(menu):
    def select_menu(menu, food):
        if food == M:
            if can_everybody_eat(menu):
                return len(menu)
            return INF
    ret = select_menu(menu, food+1)
    menu.append(food)
    ret = min(ret, select_menu(menu, food+1))
    menu.pop()
    return ret

지수시간 알고리듬

N이 하나 증가할 때 마다 걸리는 시간이 배로 증가하는 알고리즘은 지수시간(exponential time)에 동작한다고 말한다.

4.5 시간 복잡도

시간 복잡도

  • 시간 복잡도(Tiem Complexity)란 가장 널리 사용되는 알고리즘의 수행시간 기준

  • 알고리즘에 실행되는 동안 수행하는 기본적인 연산의 수를 입력의 크기에 대한 함수로 표현한 것

  • 기본적인 연산이란?

    • 더 적게 쪼개질 없는 최소 크기의 연산
      • 두 부호있는 32비트 정수의 사칙연산
      • 두 실수형 변수으 ㅣ대소 비교
      • 한 변수에 다른 변수 대입하기
    • 쪼갤수 있는 연산
      • 정수 배열 정리하기
      • 두 문자열에 서로 같은지 확인하기
      • 입력된 두 소인수 분해하기

  • 시간 복잡도가 높다 = 입력의 크기가 증가할 때 알고리즘의 수행시간이 더 빠르게 증가

    -> 시간 복잡도가 낮다고 해서 언제나 더 빠르게 증가하는 것은 아님!

입력의 종류에 따른 수행시간의 변화

  • 입력이 어떤 형태로 구성되어 있는지도 수행시간에 영향
  • eg) 선형 탐색
    • 운 좋게 처음에 찾을 수 있고/ 운 나쁘면 마지막에 찾을 수 도 있음
    • 최선의 수행시간:
      • 찾으려는 원소가 맨 앞에 있음
      • 반목문의 수행 횟수: $1$
    • 최악의 수행시간:
      • 배열에 해당 원소가 없을 때 알고리즘은 $N$번 반복하고 종료
      • 반목문의 수행 횟수: $N$
    • 평균적인 경우의 수행시간:
      • 평균적인 경우의 수행시간을 분석하기 위해서는 존재할 수 있는 모든 입력의 등장 확률이 모두 같다고 가정
      • 만약 주어진 배열이 항상 원소를 포함한다고 가정하면 반환 값의 기대값은 $2 \over N$
      • 평균적인 수행 횟수: $2 \over N$
    • 대게 사용하는 것은 최악의 수행시간 혹은 수행시간의 기대치
      • 많은 경우 이 두 기준은 따로 구분하지 않고 쓰인다
      • 여러 알고리즘에서 이 두 기준은 거의 같음

점근적 시간 표기: $O$ 표기

  • 대문자 $O$ 표기 (Big-O Notation)
    • 주어진 함수에서 가장 빨리 증가하는 항만을 남긴채 나머지를 다 버리는 표기법
  • $O$ 표기법 의미
    • $O$ 표기법은 대략적으로 함수의 상한을 나타낸다.
    • $N$에 대한 함수 $f(N)$에 주어질 때, $f(N)=O(G(N))$이라고 쓰는 것은 아주 큰 $N_0$와 $C(N_0,C>0)$를 적절히 선택하면 $N_0 \lt N)인 모든 $N$에 대해
      $\left| f(N) \right| \le C*\left| g(N) \right| $ 이 참이 되도록 할 수 있다.
© 2020 - 2022 Aiden's Camp
Built with Hugo
Theme Stack designed by Jimmy