알고리즘 문제 해결 전략을 읽고 요약했습니다.

5. 알고리즘의 정당성 증명

5.1 도입

알고리즘의 정당성 증명

단위 테스트
- 알고리즘에 문제가 있음을 증명할 수는 있어도 문제가 없음을 증명할 수는 없음
다른 방법이 필요

5.2 수학적 귀납법과 반복문 불변식

eg) 100개의 도미노가 있고 다음 두가지 사실을 안다고 가정

첫 번째 도미노는 직접 손으로 밀어서 쓰러트인다.
한 도미노가 쓰러지면 다음 도미노 역시 반드시 쓰러진다.

-> 마지막 도미노 또한 당연히 쓰러진다.
-> 직관적으로 알 수 있음

수학적 귀납법

Mathmetical Induction
반복적인 구조를 갖는 명제들을 증명하는데 유용하게 사용되는 증명 기법

귀납법 단계

단계 나누기
- 증명하고 싶은 사실을 여러 단계로 나눈다.
- 100개의 도미노를 하나씩 나눔
첫 단계 증명
- 첫 단계에서 증명하고 싶은 내용이 성립함을 보인다.
- 첫 번째 도미노가 넘어짐을 증명
귀납 증명
- 다음 단계에서도 성립함을 보인다.
- 한 도미노가 쓰러지면 다음 도미노는 반드시 쓰러짐

사다리 게임

맨 위와 맨 아래가 1:1 대응이다. imgs

단계 나누기
- 텅 빈 $N$개의 세로줄에서부터 시작해서 원하는 사다리가 될 때까지 하나씩 가로줄을 그어 간다. 이때, 가로즐을 하나 긋는 것을 한 단계라고 정의
첫 단계 증명
- 텅 빈 $N$개의 세로줄에서는 맨 위 선택지와 맨 아래 선택지가 1:1 대응
- 첫 번째 도미노가 넘어짐을 증명
귀납 증명
- 가로 줄을 그어서 두 개의 세로줄을 연결, 이 때 두 세로줄의 결과는 서로 뒤바뀐다.
- 두 세로줄의 결과가 바뀌어도 1:1 대응은 변하지 않는다
- -> 다음 단계에서도 1:1 대응 특성 유지

-> 따라서 귀납법에 의해 가로줄만을 사용하는 사다리들은 항상 1:1 대응된다.

반복문 불변식

귀납법은 알고리즘의 정당성을 증명할 때 가장 유용하게 사용되는 기법이다.

대부분의 알고리즘은 어떠한 형태로든 반복적인 요소를 가지고 있기 때문이다.
귀납법은 이런 알고리즘들이 옳은 답을 계산함을 보이기 위해서
- 알고리즘의 각 단계가 정답으로 가는 길 위에 있음을 보이고
- 결과적으로는 알고리즘의 답이 옳음을 보인다.

반복분 불변식

반복문의 내용이 한 번 실행될 때 마다 중간 결과가 우리가 원하는 답으로 가는 길 위에 잘 있는지를 명시하는 조건
반복문이 마지막에 정답을 계산하기 위해서는 항상 이 식이 변하지 않고 성립해야 한다.

불변식을 이용한 반복문의 정당성 증명

반복문 진입시에 분변식이 성립함을 보인다.
반복문 내용이 불변식을 깨뜨리지 않음을 보인다.
- 반복문 내용이 시작할 때 분변식이 성립했다면 내용이 끝날때도 불변식이 항상 성립함을 보인다.
반복문 종료시에 불변식이 성립하면 항상 우리가 정답을 구했음을 보인다.

eg) while문

1
2
3
4
5
6
# 불변식은 여기에서 성립해야 한다.
while 어떤 조건:
    # 반복문 내용의 시작
    ...
    # 반복문 내용의 끝
    # 불변식은 여기에서도 성립해야 한다.

이진 탐색과 반복분 불변식

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
# 필수 조건: A는 오름차순으로 정렬되어 있다.
# 결과: A[i-1] < x <= A[i]인 i를 반환한다.
# 이 때 A[-1]=음의 무한대, A[N]=양의 무한대라고 가정한다.
def binsearch(A, x):
    n = len(A)
    lo = -1
    hi = n
    # 반복문 불변식 1: lo < hi
    # 반복문 불변식 2: A[lo] < x <= A[hi]
    while lo+1 < hi:
        mid = (lo+hi)//2
        if A[mid] < x:
            lo = mid
        else:
            hi = mid
    return hi

$lo+1=hi$
- while 문이 종료된다.
  - $lo+1 \ge hi$
  - 불변식에 의하면 $lo < hi$이니, $lo+1 = hi$
  - $A[lo] < x \le A[hi]$: 불변식 성립
초기 조건
- while 문이 시작할 때 lo, hi는 초기값 -1, n으로 초기화된 상태
- 만약 n=0이라면 while문을 건너 뛰게 됨 -> 불변식 1 성립
- $A[-1] = -\infty, A[N]=\infty$라고 가정 -> 불변식 2 성립
유지 조건
- while 문 내부가 불변식을 깨뜨리지 않음
- 불변식 1
  - while문 내부로 들어옴
  - -> hi와 lo의 차이가 2 이상
  - -> mid는 항상 두 값 사이에 위치
  - -> mid를 lo,hi 어디에 대입해도 항상 불변식 1은 성립
- 불변식 2
  - $A[mid] < x$인 경우
    - 반복문을 시작할 때 $x \le A[hi]$임을 알고 있음
    - -> $A[mid] < x \le A[hi]$이므로, lo에 mid를 대입해도 불변식 2는 성립
  - $x \le A[mid]$인 경우
    - $A[lo] < x$와 합치면
    - -> $A[lo] < x \le A[mid]$
    - -> hi에 mid를 대입해도 불변식 2는 성립

삽입 정렬과 반복문 불변식

구현 코드

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def insertion_sort(A):
    for i in range(len(A)):
        # 불변식 a: A[0, ..., i-1]은 이미 정렬되어 있다.
        # A[0, ..., i-1]에 A[i]를 끼워 넣는다.
        j = i
        while j > 0 and A[j-1] > A[j]:
            # 불변식 b: A[j+1, ..., i]의 모든 원소는 A[j]보다 크다.
            # 불변식 c: A[0, ..., i]구간은  A[j]를 제외하면 정렬되어 있다.
            A[j], A[j-1] = A[j-1], A[j]
            j -= 1

초기 조건: 반복문이 시작할 때 i=0이면 해당 구간은 비어 있으니 항상 정렬되어 있다고 가정한다.
불변식 유지: for문의 내용이 종료할 때 이 불변식이 깨지지 않고 유지됨을 보이기 위해서는 while문의 정당성을 증명

eg) 이해를 위한 example

i = 0
- 불변식 a
  - A[0, ... -1]은 정렬되어 있다.
  - A[0, ... -1]에 A[0]를 끼어 넣는다.
- j = 0
  - while문 스킵
i = 1
- 불변식 a
  - A[0, ... 0]은 정렬되어 있다.
  - A[0, ... 0]에 A[1]를 끼어 넣는다.
- j = 1
  - j > 0 and A[0] > A[1]
  - A[0, 1] <- sorted
i = 2
- 불변식 a
  - A[0, ... 1]은 정렬되어 있다.
  - A[0, ... 1]에 A[2]를 끼어 넣는다.
- …

초기 조건

$j=0$
- $j=0$ 이라면 불변식 (b)에 의해 $A[j]$가 $A[0, …, i]$ 구간 중 가장 작은 수가 된다.
- 불변식 (c)와 합쳐 보면 $A[0, …, i]$ 구간 전체가 정렬되어 있다.
$j>0$
- $j>0$이고 $A[j-1] \le A[j]$라면, 불변식 (b)와 합쳐 $A[j-1] \le A[j] < A[j+1]$ 가 된다.
- 불변식 (c)와 합쳐 보면 $A[0, …, i]$ 구간 전체가 정렬되어 있다.

불변식 유지

(b)와 (c)가 항상 성립함을 증명

(b) 초기 조건: while 문 진입시에 $A[j+1, …, i]$ 구간은 (빈 구간)(j+1==i)이므로 (b)는 참
(b) 유지 조건: while 문 내용이 실행되었다는 말은 $A[j-1]>A[j]$ 라는 의미. 이 둘을 교체하고 $j$를 1 줄이면 (b)는 여전히 참
(c) 초기 조건: 불변식 (a)에 의해 구간 $A[0, …, i-1]]$은 항상 정렬되어 있으니 while문 진입 초기시에는 (c)는 항상 참
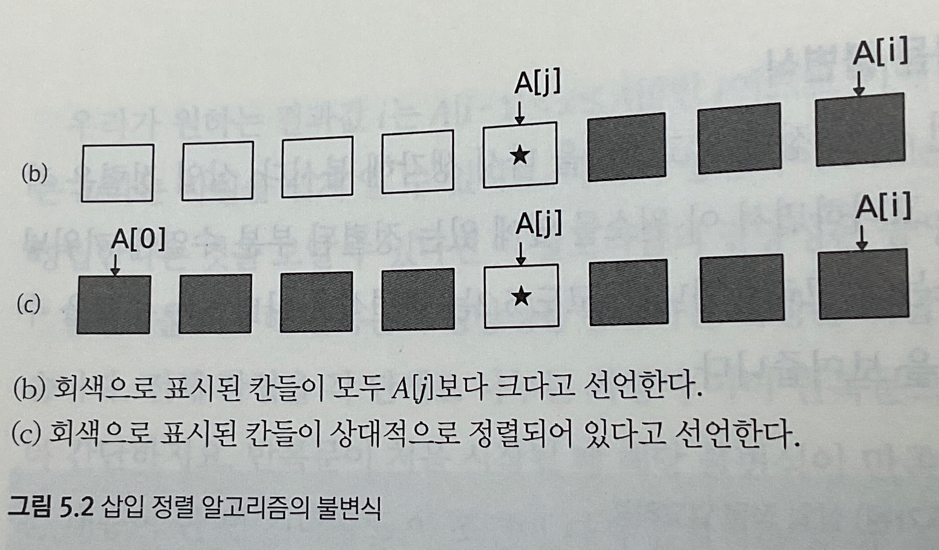
(c) 유지 조건: 그림 (c)에 $A[j]$ 와 이전 원소를 교체한다고 해도 회색 원소들 간의 상대적 순서는 변하지 않기에 (c)는 항상 참

단정문을 이용해 반복문 불변식 강제하기

불변식을 주석으로만 달아두는 것이 아니라 단정문으로 강제 -> 불변식이 깨지면 프로그램이 종료되게해서 불변식이 깨졌음을 쉽게 알 수 있음

5.3 귀류법

우리가 원하는 바와 반대되는 상황을 가정하고 논리를 전개해서 결론이 잘못 됏음을 찾아내는 증명 기법
어떤 선택이 항상 최선임을 증명하고자 할 때 많이 이용됨
- -> 우리가 선택한 답보다 좋은 답이 있다고 가정한 후에, 사실 그럴일이 있을 수 없음을 보이면 우리가 최선의 답을 선택했음을 보임

책상 쌓기

$Q)$ 상장 형태로 된 책장을 여러 개 쌓아 올릴려고 한다.
각 책장마다 버틸수 있는 최대 무게 $M_i$와 자신의 무게 $W_i$가 주어진다.
이 때 책장을 가장 높이 쌓는다면 몇 개나 쌓을 수 있을까?
단, $above(i)$가 $i$번 책상 위에 쌓인 모든 책장의 집합이라고 할 때, 다음이 성립해야 한다. $$\sum_{j\in above(i)}{w_j \le M_i}$$

-> 책상위에 올라간 다른 책장들의 무게의 합이 견딜 수 있는 최대 무게를 초과하면 안 된다.

$A)$ what if? 항상 무거운 책장을 아래 쪽에 쌓는 것이 좋다는 사실을 알고 있다.
-> 주어진 책상들을 정렬 후 순서에 신경 쓰지 않고 어느 책장을 고를지만 집중
-> $M_i$로 정렬? $W_i$로 정렬?
-> 정답은 $M_i + W_i$가 큰 것부터 아래에

$Proof)$
$M_i + W_i$가 더 큰 책장 A가 더 작은 책장 B에 올라간 형태
-> A와 B의 위치를 항상 바꿀 수 있음을 증명

$$M_A > M_B + W_B - W_A$$ A 위에 올라가 있는 상자들의 무게의 합 = $X$ $$M_B > M_A + X$$ => $$M_A > M_B + W_B - W_A \ge + X + W_B$$

A도 B와 나머지 모든 상자를 지탱할 수 있음.
따라서, 우리가 원하는 순서대로 쌓을 때 가장 높은 탑을 알지 못할 경우의 수는 존재하지 않는다.

5.4 다른 기술들

비둘기 집의 원리

Pigeonhole Principla
10 마리의 비둘기가 9개의 비둘기 집에 들어 깟다면, 2 마리 이상이 들어간 비둘기 집은 반드시 하나 있기 마련이다.

동전 뒤집기

100개의 동전이 바닥에 깔려 있는데 이 중 $F$개는 앞면, $100-F$개는 뒷면이다.
이 동전들이 모두 앞면으로 오게 하고 싶은데, 한 번 뒤집을 때 반드시 $X$개를 뒤집어야 한다.
이 때 뒤집는 횟수를 최소화 하고 싶을 때 답의 상한은?
=> 100

순환 소수 찾기

분수 $\frac{a}{b}$가 주어졌을 때 실수 연산을 사용하지 않고 이 분수를 소수 형태로 출력하려고 한다.
eg) $\frac{3}{8}=0.375$, $\frac{4912}{400}=11.78$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
# 분수 a/b의 소수 표현을 출력한다.
# a>=0, b>0 이라고 가정함
def print_demical(a, b):
    ret = ""
    i = 0
    while a > 0:
        # 첫 번째와 두 번째 사이에 소수점을 찍는다.
        i += 1
        if i == 1:
            ret += "."
        ret += str(a//b)
        a = (a % b) * 10
    print(ret)

if) $\frac{1}{11}$이 입력 -> $0.090909…$ 무한 소수

a%b의 결과는 언제나 [0, b-1] 범위의 값을 가정한다.
while문이 b+1번 반복될 때까지 함수가 종료되지 않음
- -> a%b의 결과는 b가지의 결과를 가질 수 있음
- -> 결과가 중복되는 경우가 반드시 있음

구성적 증명

Constructive Prrof
우리가 원하는 어떤 답이 존재한다는 사실을 증명하기 위해 사용
답이 존재한다는 사실을 노증하는 것(귀납법, 귀류법) <=> 답의 실제 예를 들거나 만드는 방법을 제시하는 증명(구성적 증명)

안정적 결혼 문제

문제 풀이 알고리즘

처음에는 여성들이 모두 자신이 가장 선호하는 남성의 앞에 가서 프러포즈를 한다. 남성이 그 중 제일 마음에 드는 여성을 고르면 나머지는 제자리로 돌아간다.
제자리도 돌아간 여성들이 (상대에게 짝이 있던 없던 관계없이) 다음으로 마음에 드는 남성에게 프러포즈한다. 남성은 현재 자기 짝보다 마음에 드는 여성이 다가오면, 현재 짝을 돌려 보낸다.
더 프러포즈를 할 여성이 없을 때까지 2를 반복한다.

증명

종료 증명
- 각 여성은 돌아갈 때 마다 지금까지 프러포즈했던 남성들보다 우선 순위가 낮은 남성에게 프러포즈한다.
- 따라서 각 여성이 최대 $n$명의 남성들에게 순서대로 프러포즈한 이후에는 더 이상 프러포즈를 할 남성이 없으므로, 이 과정을 언젠간 반드시 종료한다.
모든 사람이 짝을 찾는지 증명
- 프러포즈를 받은 남성은 그 중 한 사람을 반드시 선택하고, 더 우선순위가 높은 여성이 프러포즈해야만 짝을 바꾸므로 한 번이라도 프러포즈를 받은 남성은 항상 짝이 있다.
- 귀류법을 적용
  - 남녀 한 사람씩 짝을 못 찾음
  - 여성은 우선순위가 높은 순서대로 모두에게 프러포즈하기 때문에 이 남성에게 프러포즈
  - 남성은 프러포즈를 받아 들여야 함
  - 짝을 찾지 못하는 사람은 있을 수 없음
짝들의 안정성
- 귀류법
  - 짝이 아닌 두 남녀가 서로 자신의 짝보다 상대방을 더 선호한다고 가정
  - 여성은 지금 자신의 짝 이전에 그 남성에게 반드시 프러포즈 했어야 함
  - 그런데도 이 남성이 이 여성과 짝 지어지지 않았따는 것은 더 마음에 드는 여성에게 프러포즈 받아서 수락함
  - 프러포즈 받았떤 여성보다 맘에 들지 않은 여성과 최종적으로 짝이 되는일은 없음