algorithm

6. 무식하게 풀기

알고리즘 문제 해결 전략을 읽고 요약했습니다.

6. 무식하게 풀기

6.1 도입

무식하게 풀기

  • Brute Force
  • 컴퓨터의 빠른 계산 능력을 이용해 가능한 경우의 수를 일일이 나열하면서 답을 찾는 방법

완전 탐색

  • Exhaustive search
  • 컴퓨터의 장점을 이용한 방법

6.2 재귀호출과 완전탐색

재귀 함수

  • Recursive Function
  • 자신이 수행한 작업을 유사한 형태의 여러 조각으로 쪼갠 뒤 그 중 한 조각을 수행하고, 나머지를 자기 자신을 호출해 실행하는 함수

eg) 1부터 n까지의 합을 구하는 함수

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

# 필수 조건: n>=1
# 결과: 1부터 n까지의 합을 반환한다.
def n_sum(n):
    ret = 0
    for i in range(1, n+1):
        ret += i
    return ret

# 필수 조건: n>=1
# 결과: 1부터 n까지의 합을 반환한다.
def recursive_sum(n):
    if n == 1:
        return n
    return n + recursive_sum(n-1)
  • n개의 숫자의 합을 구하는 작업을 n개의 조각으로 쪼개, 더할 각 숫자가 하나의 조각이 되도록 한다.
  • 재귀 호출을 이용하기 위해서는 이 조각 중 하나를 떼어내어 자신이 해결하고, 나머지 조각들을 자기 자신을 호출해서 해결한다.
  • 모든 재귀 함수는 ‘더 이상 쪼개지지 않는’ 최소한의 작업에 도달 했을 때 답을 곧장 반환하는 조건문을 포함한다.
    • 쪼개기지 않는 가장 작은 작업들 : 기저 사례 (base case)

예제: 중첩 반복문 대체하기

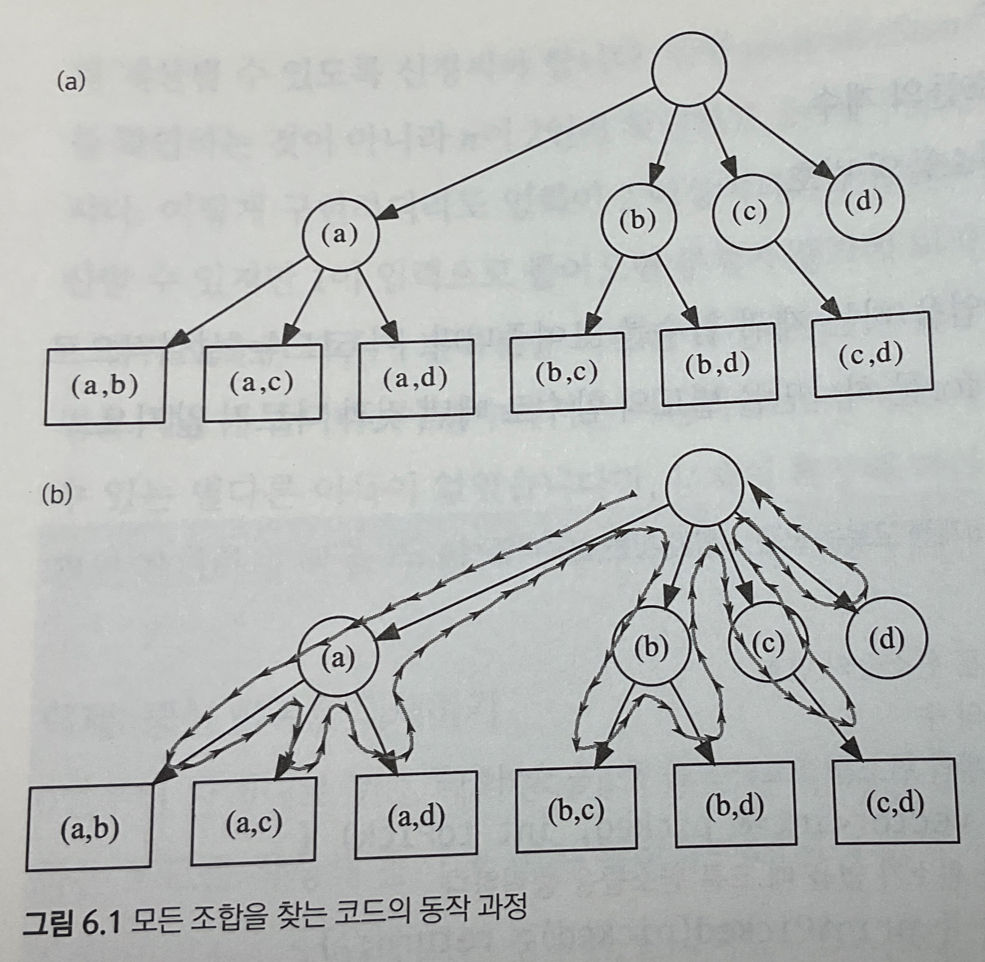
eg) 0번 부터 차례대로 번호 매겨진 n개의 원소 중 네 개를 고르는 모든 경우를 출력하라

1
2
3
4
5

for i in range(n):
    for j in range(i+1, n):
        for k in range(j+1, n):
            for l in range(k+1, n):
                print(i, j, k, l)
  • if) 5개? -> 5중 for 문
  • if) 6개? -> 6중 for 문
  • 중첩 for문
    • 골라야 할 원소의 수가 늘어날수록 코드가 길고 복잡해진다.
    • 골라야 할 원소의 수가 입력에 따라 달라질 수 있는 경우 사용할 수 없다.

-> 재귀 호출

  • 위 코드 조각이 하는 일을 네 개의 조각으로 나눌 수 있다.
  • 각 조각에서 하나를 고르고 남은 원소들을 고르는 작업을 자기 자신을 호출해 떠넘기는 재귀함수
  • 남은 원소를 고르는 ‘작업’을 다음과 같은 입력들의 집합으로 정의
    • 원소들의 총 개수
    • 더 골라야 할 원소의 개수
    • 지금까지 고른 원소의 번호
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# n: 전체 원소의 수
# picked: 지금까지 고른 원소들의 번호
# to_pick: 더 고를 원소의 수
def pcik(n, picked, to_pick):
    # 기저 사례: 더 고를 원소가 없을 때 고른 원소들을 출력한다.
    if to_pick == 0:
        print_picked(pick)
        return
    # 고를 수 있는 가장 작은 번호를 계산한다.
    smallest = 0 if len(pick) == 0 else pcik[-1] + 1
    # 이 단계에서는 원소 하나를 고른다.
    for next_n in range(smallest, n):
        picked.append(next_n)
        pick(n, picked, to_pick - 1)
        picked.pop()

img

예제: 보글 게임

img Q)
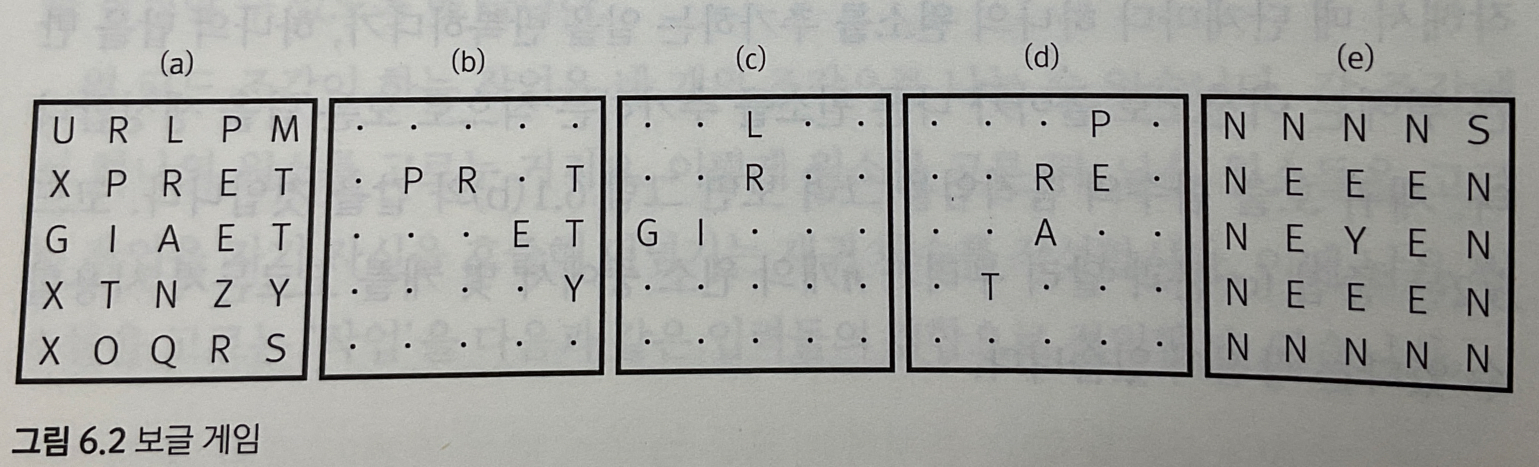
보글(Boggle)은 그림 6.2(a)와 같은 5x5 크기의 알파벳 격자를 가지고 하는 게임
게임의 목적은 상하좌우/ 대각선으로 인접한 글자들을 이어서 단어를 찾아내는 것
eg) PRETTY, GIRL, REPEAT
각 글자들을 대각선으로도 이어질 수 있으며, 한 글자가 두 번 사용될 수도 있다.
-> has_word(y, x, word)

  • 문제의 분할
    • 각 글자를 하나의 조각으로 만드는 것
  • 기자 사례의 선택
    • 더 이상의 탐색 없이 간단히 답을 낼 수 있는 다음의 경우를 기저 사례로 선택
      1. 위치 (y, x)에 있는 글자가 원하는 단어의 첫 글자가 아닌 경우 항상 실패
      2. (1번에 해당되지 않을 경우) 원하는 단어가 한 글자인 경우 성공
  • 구현
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

    dx = [-1, -1, -1, 1, 1, 1, 0, 0]
dy = [-1, 0, 1, -1, 0, 1, -1, 1]
def has_word(y, x, word):
    if not in_range(y, x):
        return False
    if board[y][x] != word[0]:
        return False
    if len(word) == 1:
        return True
    for direction in range(8):
        new_y = y + dy[direction]
        new_x = x + dx[direction]
        if has_word(new_y, new_x, word[1:]):
            return True
    return False
  • 시간 복잡도 분석
    • 완전 탐색 알고리즘의 시간 복잡도 -> 가능한 모든 경우의 수를 전부 세보기
    • if) 전부 A인 격자에서 AAAAAH 찾기
      • 답이 없는 경우
      • $8^{N-1}=O(8^N)$

완전 탐색 레시피

어떤 문제를 완전 탐색으로 해결하기 위해 필요한 과정

  1. 단계
    • 완전 탐색은 존재하는 모든 답을 하나씩 검사하므로, 걸리는 시간은 가능한 답의 수에 정확히 비례
    • 최대 크기의 입력을 가정했을 때 답의 개수를 계산하고 이들을 모두 제한 시간 안에 생성할 수 있을 지를 가늠
    • 만약 시간안에 계산할 수 없다면 설계 패러다임(추후 설명)을 적용
  2. 단계
    • 가능한 모든 답의 후보를 만드는 과정을 여거래의 선택으로 나눈다.
    • 각 선택은 답의 호부를 만드는 과정의 한 조각
  3. 단계
    • 그 중 하나의 조각을 선택해 답의 일부를 만들고, 나머지 답을 재귀 호출을 통해 완성
  4. 단계
    • 조각이 하나 밖에 남지 않은 경우, 혹은 하나도 남지 않은 경우에는 답을 생성 했으므로, 이것을 기저 사례로 선택해 처리

이론적 배경: 재귀 호출과 부분문제

문제와 부문문제

예시)

  • 문제: 주어진 자연수를 정렬하라
  • 문제: ${16, 7, 9, 1, 31}$을 정렬하라

차이점: 전자는 입력을 지정하지 않고 후자는 특별한 입력 지정

보글 게임 예시)

  1. 현재 위치 (y, x)에 단어의 첫글자가 있는가?
  2. 윗 칸에서 시작해서, 단어의 나머지 글자를 찾을 수 있는가?
  3. …
  4. …
  • 2번 이후
    • 원래 문제에서 한 조각을 떼어 냈을 뿐, 형식이 같은 또 다른 문제를 푼 결과
    • 문제를 구성하는 조각들 중 한 조각을 뺏기 때문에, 이 문제들은 원래 문제의 일부
    • -> 이런 문제들을 원래의 부분문제

6.7 최적화 문제

  • 문제의 답이 하나가 아니라 여러 개이고, 그 중에서 어떤 기준에 따라 가장 좋은 답을 찾아내는 문제
  • eg) $n$개의 원소 중 $r$개를 순서없이 골라내는 문제
    • 최적화 문제 x
    • 우리가 원하는 답은 딱 하나 밖에 없다 -> 더 좋은 답이나 덜 좋은 답이 없음
  • eg) $n$개 사과 중 $r$개 골라서 무게의 합을 최대화하는 문제
    • 최적화 문제
  • 최적화 문제 해결 방법
    • 완전 탐색
    • 동적 계호기법
    • 조합 탐색
    • 최적화 문제 -> 결정 문제로 변환

예제: 여행하는 예판원 문제 (Traveling Salssman Problem, TSP)

어떤 나라에 $n(2 \le n \le 10)$개의 큰 도시가 있다. 한 영업사원이 한 도시에서 출발해 다른 도시들을 전부 한 번씩 방문한 뒤 시작 도시로 돌아오려고 한다. 각 도시들은 모두 직선도로로 연결되어 있다. 영업사원이 여행해야 할 거리 중 가장 짧은 경로는 ?

무식하게 풀 수 있을까?

시간안에 답을 구할 수 있을까?
-> $(n-1)!$ -> $9!$ -> $362,880$ -> 1초안에 처리할 수 있는 숫자

재귀 호출을 통한 답안 생성

  • $n$개의 도시로 구성된 경로를 $n$개의 조각으로 나눠 앞에서부터 도시를 하나씩 추가해 경로를 만들기
  • shortest_path(path)=path -> 지금까지 만든 경로, 나머지 도시를 모두 방문하는 경로들 중 가장 짧은 것을 반환한다.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def shortest_path(path, visited, current_length):
    # 기저 사례: 모든 도시를 다 방문했을 때는 시작도시로 돌아가고 종료
    if len(path) == n:
        return current_length + dist[path[0]][path[-1]]
    ret = 987654321
    for next_visit in range(n):
        if visited[next_visit]:
            continue
        here =path[-1]
        path.append(next_visit)
        visited[next_visit] = True
        cand = shorted_path(path, visited, current_length + dist[here][next_visit])
        ret = min(ret, cand)
        visited[next_visit] = False
        path.pop()
    return ret
© 2020 - 2022 Aiden's Camp
Built with Hugo
Theme Stack designed by Jimmy