Wasserstein GAN
이번 페이지에서는 기존 GAN 에서 사용하던 Mean Squared Error 를 수정해 학습 안정성을 확보한 Wasserstein GAN 에 대해서 구현합니다.
Paper
논문에서 제시하는 최적화 알고리즘은 다��음과 같습니다.

기존 DCGAN 에서 사용한 학습 코드를 수도코드로 작성하면 다음과 같습니다.
for epoch in range(n_epochs):
for batch in loader:
#
# 1. get discriminator loss from real data
#
...
#
# 2. get discriminator loss from fake data
#
...
#
# 3. get discriminator loss and update discriminator
#
...
#
# 4. get generator loss and update generator
#
...
Wasserstein 알고리즘을 Python 수도 코드로 작성하면 다음과 같습니다.
for epoch in range(n_epochs):
for step, batch in enumerate(loader):
#
# 1. get discriminator loss from real data
#
...
#
# 2. get discriminator loss from fake data
#
...
#
# 3. get discriminator loss and update discriminator
#
...
#
# 4. clip weight
#
...
if step % n_critic == 0: # in paper suggested n_critic is 5
#
# 5. get generator loss and update generator
#
...
학습기를 학습한 이후 파라미터를 주어진 값으로 최소와 최대값을 제한합니다. 논문에서는 이 값을 로 제시했습니다.
for epoch in range(n_epochs):
for step, batch in enumerate(loader):
...
#
# 4. clip weight
#
...
논문에서는 분류기의 학습이 만큼 진행 후 생성기를 학습하도록 제안했습니다. 이를 위해서 주어진 step 의 나머지가 0이 될 때 생성기를 학습하는 분기를 선언합니다.
for epoch in range(n_epochs):
for step, batch in enumerate(loader):
...
if step % n_critic == 0: # in paper suggested n_critic is 5
#
# 5. get generator loss and update generator
#
...
Dataset
우선 튜토리얼에 들어가기에 앞서 사용할 데이터셋을 선언합니다. 데이터셋에 대한 자세한 설명은 CelebA 페이지에서 확인할 수 있습니다.
우선 배치 사이즈를 논문에서 제시하는 mini batch 숫자와 맞추기 위해 64로 설정합니다.
또한 배치 사이즈가 다를 경우 의도한 대로 학습이 안 될 수 있기 때문에 64가 안될 수 있는 마지막 배치는 사용하지 않도록 drop_last=True 로 선언합니다.
import torchvision.transforms as T
import numpy as np
import matplotlib.pyplot as plt
from torchvision.datasets.celeba import CelebA
from torch.utils.data import DataLoader
from torchvision.utils import make_grid
transform = T.Compose(
[
T.Resize(64),
T.CenterCrop(64),
T.ToTensor(),
T.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
]
)
dataset = CelebA(
"./datasets", download=True, transform=transform
)
loader = DataLoader(dataset, batch_size=64, shuffle=True, drop_last=True)
Model
WGAN 에서는 학습 방법만 수정을 하기 때문에 모델은 DCGAN 에서 사용한 모델을 그대로 사용합니다. 생성기와 분류기에 대한 자세한 설명은 DCGAN 페이지에서 확인할 수 있습니다.
Generator
import torch
import torch.nn as nn
class Generator(nn.Module):
def __init__(self, num_channel=3, latent_dim=100, feature_dim=64):
super().__init__()
self.layer_1 = nn.Sequential(
nn.ConvTranspose2d(latent_dim, feature_dim * 8, 4, 1, 0, bias=False),
nn.BatchNorm2d(feature_dim * 8),
nn.ReLU(True),
)
self.layer_2 = nn.Sequential(
nn.ConvTranspose2d(feature_dim * 8, feature_dim * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(feature_dim * 4),
nn.ReLU(True),
)
self.layer_3 = nn.Sequential(
nn.ConvTranspose2d(feature_dim * 4, feature_dim * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(feature_dim * 2),
nn.ReLU(True),
)
self.layer_4 = nn.Sequential(
nn.ConvTranspose2d(feature_dim * 2, feature_dim, 4, 2, 1, bias=False),
nn.BatchNorm2d(feature_dim),
nn.ReLU(True),
)
self.last_layer = nn.Sequential(
nn.ConvTranspose2d(feature_dim, num_channel, 4, 2, 1, bias=False),
nn.Tanh(),
)
def forward(self, z):
# decoding
layer_1_out = self.layer_1(z) # (N, 512, 4, 4)
layer_2_out = self.layer_2(layer_1_out) # (N, 256, 8, 8)
layer_3_out = self.layer_3(layer_2_out) # (N, 128, 16, 16)
layer_4_out = self.layer_4(layer_3_out) # (N, 64, 32, 32)
# transform to rgb
out = self.last_layer(layer_4_out) # (N, 3, 64, 64)
return out
Discriminator
WGAN 에서는 바뀐 학습 방법에 따라서 Discriminator 를 �바꿔야 합니다. 논문에서는 Critic 이라는 표현을 쓰지만 다른 GAN 과의 통일성을 위해서 여기서는 Discriminator 로 사용하겠습니다.
class Discriminator(nn.Module):
def __init__(self, num_channel=3, feature_dim=64):
super().__init__()
self.layer_1 = nn.Sequential(
nn.Conv2d(num_channel, feature_dim, 4, 2, 1, bias=False),
nn.BatchNorm2d(feature_dim),
nn.LeakyReLU(0.2, inplace=True),
)
self.layer_2 = nn.Sequential(
nn.Conv2d(feature_dim, feature_dim * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(feature_dim * 2),
nn.LeakyReLU(0.2, inplace=True),
)
self.layer_3 = nn.Sequential(
nn.Conv2d(feature_dim * 2, feature_dim * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(feature_dim * 4),
nn.LeakyReLU(0.2, inplace=True),
)
self.layer_4 = nn.Sequential(
nn.Conv2d(feature_dim * 4, feature_dim * 8, 4, 2, 1, bias=False),
nn.BatchNorm2d(feature_dim * 8),
nn.LeakyReLU(0.2, inplace=True),
)
self.last_layer = nn.Sequential(
nn.Conv2d(feature_dim * 8, 1, 4, 1, 0, bias=False)
)
def forward(self, x):
# encoding
layer_1_out = self.layer_1(x) # (N, 64, 32, 32)
layer_2_out = self.layer_2(layer_1_out) # (N, 128, 16, 16)
layer_3_out = self.layer_3(layer_2_out) # (N, 256, 8, 8)
layer_4_out = self.layer_4(layer_3_out) # (N, 512, 4, 4)
# classify
out = self.last_layer(layer_4_out).squeeze() # (N)
return out
가장 큰 차이점은 이제 마지막 layer 의 출력값에 sigmoid 를 사용하지 않습니다.
논문에서는 다음과 같이 설명합니다.
This is due to the fact that mode collapse comes from the fact that the optimal generator for a fixed discriminator is a sum of deltas on the points the discriminator assigns the highest values, as observed by [4] and highlighted in [11].
이와 관련해서 논문에서는 BCELoss 를 사용할 때 판별자가 Real/Fake 구분이 너무 쉬워지기 때문에, GAN 의 고질적인 문제인 Mode Collapse 문제가 생긴다고 설명합니다. 그래서 이러한 BCELoss 대신 Wasserstein Loss 를 제시합니다.
- The Earth-Mover (EM) distance or Wasserstein-1
이러한 내용 때문에 분류기의 마지막 layer 에서 sigmoid 를 사용하지 않습니다.
WGAN Train
이제 위에서 작성한 수도 코드의 내용을 채워서 학습을 진행해 보겠습니다.
Weight Initialization
DCGAN 에서 적용했던 내용을 같이 설정합니다.
파라미터 초기화를 위한 함수를 작성합니다.
def weights_init(m):
classname = m.__class__.__name__
if classname.find("Conv") != -1:
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find("BatchNorm") != -1:
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
각 모델에 적용합니다.
_ = generator.apply(weights_init)
_ = discriminator.apply(weights_init)
Convolution Network 는 원활한 학습을 위해서는 gpu 가 필요합니다. GPU 가 없는 경우 학습에 다소 시간이 소요될 수 있습니다.
아래 코드를 이용해 device 를 선언합니다.
만약 gpu 가 사용 가능한 경우 device(type='cuda') 메세지가 나옵니다.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
device
device(type='cuda')
위에서 선언한 모델을 gpu 메모리로 옮기겠습니다.
_ = discriminator.to(device)
_ = generator.to(device)
Logger
학습 과정을 tensorboard 에 저장하기 위한 writer 입니다.
from torch.utils.tensorboard import SummaryWriter
# tensorboard logger
writer = SummaryWriter()
Loss
위의 Discriminator 에서 설명한 것 과 같이 WGAN 에서는 loss term 을 분류기의 거리의 평균을 이용하기 때문에 따로 선언하지 않습니다.
Optimizer
논문에서는 제시하는 RMSProp 을 사용하며 learning_rate 또한 제시된 0.00005 를 사용합니다.
import torch.optim as optim
# optimizer
discriminator_opt = optim.RMSprop(discriminator.parameters(), lr=0.00005)
generator_opt = optim.RMSprop(generator.parameters(), lr=0.00005)
Code
from tqdm import tqdm
# for meta
n_epochs = 5
n_critic = 5
weight_cliping_limit = 0.01
# for visualization
iteration = 0
fixed_z = torch.randn((64, latent_dim, 1, 1)).to(device)
# for iteration history
G_loss_history = []
D_loss_history = []
# train code
for epoch in range(n_epochs):
epoch_G_loss = 0.0
epoch_D_loss = 0.0
for step, batch in enumerate(tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}")):
step += 1
generator.train()
discriminator.train()
x = batch[0].to(device)
batch_size = x.size(0)
#
# 1. get discriminator loss from real data
#
discriminator_opt.zero_grad()
real_D_score = discriminator(x)
real_D_loss = real_D_score.mean()
#
# 2. get discriminator loss from fake data
#
z = torch.randn((batch_size, latent_dim, 1, 1)).to(device)
fake_data = generator(z)
fake_D_score = discriminator(fake_data)
fake_D_loss = fake_D_score.mean()
#
# 3. get discriminator loss and update discriminator
#
D_wasserstein_loss = -real_D_loss + fake_D_loss
D_wasserstein_loss.backward()
discriminator_opt.step()
#
# 4. clip weight
#
for p in discriminator.parameters():
p.data.clamp_(
-weight_cliping_limit, weight_cliping_limit
) # in paper suggested c is 0.01
# logging
D_loss_history += [D_wasserstein_loss.item()]
epoch_D_loss += D_wasserstein_loss.item() * len(x) / len(loader.dataset)
writer.add_scalar("Loss/discriminator", D_wasserstein_loss, iteration)
#
# 5. get generator loss and update generator after n_critic
#
if step % n_critic == 0:
generator_opt.zero_grad()
z = torch.randn((batch_size, latent_dim, 1, 1)).to(device)
generated_data = generator(z)
generate_D_score = discriminator(generated_data)
G_loss = -generate_D_score.mean()
G_loss.backward()
generator_opt.step()
# logging
G_loss_history += [G_loss.item()]
epoch_G_loss += G_loss.item() * len(x) / len(loader.dataset) * n_critic
writer.add_scalar("Loss/generator", G_loss, iteration)
# iteration checkpoint
if iteration % 2000 == 0:
# visualization
with torch.no_grad():
generated_x = generator(fixed_z)
generated_x = generated_x.detach().cpu()
generated_x_grid = make_grid(generated_x, nrow=8).numpy()
generated_x_grid = (generated_x_grid * 0.5) + 0.5
generated_x_grid = np.transpose(generated_x_grid, (1, 2, 0))
plt.imsave(f"wgan-step-{iteration}.png", generated_x_grid)
# model save
torch.save(generator, f"wgan-generator-step-{iteration}.pt")
iteration += 1
log_string = f"Loss at epoch {epoch + 1} - D_loss : {epoch_D_loss:.4f}, G_loss : {epoch_G_loss:.4f}"
print(log_string)
# save last model
with torch.no_grad():
generated_x = generator(fixed_z)
generated_x = generated_x.detach().cpu()
generated_x_grid = make_grid(generated_x, nrow=8).numpy()
generated_x_grid = (generated_x_grid * 0.5) + 0.5
generated_x_grid = np.transpose(generated_x_grid, (1, 2, 0))
plt.imsave(f"wgan-step-{iteration}.png", generated_x_grid)
torch.save(generator, f"wgan-generator-step-{iteration}.pt")
poch 1/5: 0%| | 0/2543 [00:00<?, ?it/s]
Epoch 1/5: 100%|██████████| 2543/2543 [06:45<00:00, 6.28it/s]
Loss at epoch 1 - D_loss : -0.2854, G_loss : -0.3558
Epoch 2/5: 100%|██████████| 2543/2543 [06:21<00:00, 6.67it/s]
Loss at epoch 2 - D_loss : -0.2878, G_loss : -0.3582
Epoch 3/5: 100%|██████████| 2543/2543 [06:29<00:00, 6.53it/s]
Loss at epoch 3 - D_loss : -0.2777, G_loss : -0.3576
Epoch 4/5: 100%|██████████| 2543/2543 [06:17<00:00, 6.73it/s]
Loss at epoch 4 - D_loss : -0.2553, G_loss : -0.3705
Epoch 5/5: 100%|██████████| 2543/2543 [06:20<00:00, 6.69it/s]
Loss at epoch 5 - D_loss : -0.2351, G_loss : -0.3805
다음으로 계산할 것은 실제 이미지를 분류하는 부분 입니다. 앞서 Vanila GAN 에서 사용한것과 다르게 데이터 로더에서 실제 이미지를 분류기의 확률값의 평균을 loss 로 이용합니다
# train code
for epoch in range(n_epochs):
for step, batch in enumerate(tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}")):
...
x = batch[0].to(device)
#
# 1. get discriminator loss from real data
#
discriminator_opt.zero_grad()
real_D_score = discriminator(x)
real_D_loss = real_D_score.mean()
...
이어서 임의의 latent z 를 선언하고 생성기를 통해서 가짜 이미지를 만듭니다. 이후 생성된 이미지를 분류기의 확률값의 평균을 계산합니다.
# train code
for epoch in range(n_epochs):
for step, batch in enumerate(tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}")):
...
#
# 2. get discriminator loss from fake data
#
z = torch.randn((batch_size, latent_dim, 1, 1)).to(device)
fake_data = generator(z)
fake_D_score = discriminator(fake_data)
fake_D_loss = fake_D_score.mean()
...
논문에서는 분류기의 weight 를 업데이트하는 수식은 다음과 같습니다.
그렇기 때문에 두 loss 를 합쳤던 DCGAN 과 다르게 진짜 이미지의 확률값에서 생성된 이미지의 확률값을 뺀 loss 를 이용해 업데이트를 합니다.
# train code
for epoch in range(n_epochs):
for step, batch in enumerate(tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}")):
...
#
# 3. get discriminator loss and update discriminator
#
D_wasserstein_loss = real_D_loss - fake_D_loss
D_wasserstein_loss.backward()
discriminator_opt.step()
critic_D_wasserstein_loss += D_wasserstein_loss.item()
...
마지막으로 업데이트된 분류기의 파라미터를 clip 합니다.
# for meta
n_epochs = 5
n_critic = 5
weight_cliping_limit = 0.01
# train code
for epoch in range(n_epochs):
for step, batch in enumerate(tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}")):
...
#
# 4. clip weight
#
for p in discriminator.parameters():
p.data.clamp_(
-weight_cliping_limit, weight_cliping_limit
) # in paper suggested c is 0.01
...
분류기 학습의 결과물을 logging 하기 위한 코드입니다.
# train code
for epoch in range(n_epochs):
for step, batch in enumerate(tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}")):
...
# logging
D_loss_history += [D_wasserstein_loss.item()]
epoch_D_loss += D_wasserstein_loss.item() * len(x) / len(loader.dataset)
writer.add_scalar("Loss/discriminator", D_wasserstein_loss, iteration)
...
생성기는 분류기를 만큼 수행 후 업데이트 합니다.
논문에서는 생성기의 weight 를 업데이트하는 수식은 다음과 같습니다.
이를 위해서 생성된 이미지를 분류기로 분류하고 이에 대한 loss 를 앞선 분류기에서 생성된 이미지에 대해서 더한것과 반대로 평균에 -1 를 곱해서 계산합니다. 이를 통해서 분류기를 속이기 위한 gradient 값을 계산해서 생성기를 업데이트합니다.
# train code
for epoch in range(n_epochs):
for step, batch in enumerate(tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}")):
...
#
# 5. get generator loss and update generator after n_critic
#
if step % n_critic == 0:
generator_opt.zero_grad()
z = torch.randn((batch_size, latent_dim, 1, 1)).to(device)
generated_data = generator(z)
generate_D_score = discriminator(generated_data)
G_loss = -generate_D_score.mean()
G_loss.backward()
generator_opt.step()
# logging
G_loss_history += [G_loss.item()]
epoch_G_loss += G_loss.item() * len(x) / len(loader.dataset) * n_critic
writer.add_scalar("Loss/generator", G_loss, iteration)
...
아래 코드는 고정된 z 에 대해서 모델이 학습하면서 생성하는 그림이 어떻게 바뀌는지 저장하기 위한 코드입니다.
# for visualization
iteration = 0
fixed_z = torch.randn((64, latent_dim, 1, 1)).to(device)
# train code
for epoch in range(n_epochs):
...
for batch in tqdm(loader, desc=f"Epoch {epoch + 1}/{n_epochs}"):
...
# iteration checkpoint
if iteration % 2000 == 0:
# visualization
with torch.no_grad():
generated_x = generator(fixed_z)
generated_x = generated_x.detach().cpu()
generated_x_grid = make_grid(generated_x, nrow=8).numpy()
generated_x_grid = (generated_x_grid * 0.5) + 0.5
generated_x_grid = np.transpose(generated_x_grid, (1, 2, 0))
plt.imsave(f"wgan-step-{iteration}.png", generated_x_grid)
...
Loss history
Tensorboard 에 로깅된 학습 정보를 확인하면 다음과 같습니다.
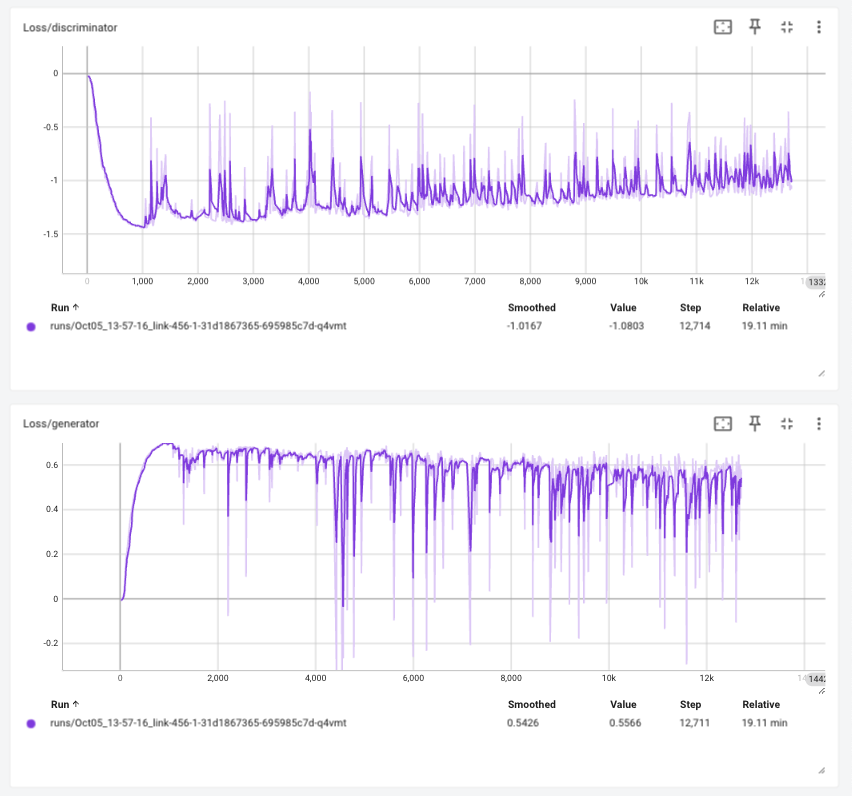
Visualize
학습을 하면서 생성기가 어떻게 이미지를 생성하는 지 확인해 보겠습니다.
import os
img_list = list(sorted(filter(lambda x: x.startswith("wgan-step"), os.listdir("."))))
step_filename = {}
for fname in filter(lambda x: x.startswith("wgan-step"), os.listdir(".")):
key = int(fname.replace("wgan-step-", "").replace(".png", ""))
step_filename[key] = fname
nrows = (len(img_list) // 3) + 1
fig, axes = plt.subplots(ncols=3, nrows=nrows, figsize=(5 * nrows, 15))
for idx, key in enumerate(sorted(step_filename)):
fname = step_filename[key]
array = plt.imread(fname)
axes[idx // 3, idx % 3].imshow(array)
axes[idx // 3, idx % 3].axis("off")
axes[idx // 3, idx % 3].set_title(fname.replace(".png", ""))
plt.tight_layout()

Generation
이번에는 학습한 모델의 디코더를 이용해 랜덤한 latent 값을 주었을 때 어떤 이미지�를 생성하는 지 확인해 보겠습니다.
다만 이번 생성기의 경우 BatchNorm 을 사용하기 때문에 학습과 평가 모드에 따라서 동작이 달라집니다.
학습이 끝난 모델을 사용하기 위해서는 eval() 모드를 설정해주어야 합니다.
generator.eval()
with torch.no_grad():
random_z = torch.randn((64, latent_dim, 1, 1)).to(device)
generated_x = generator(random_z)
generated_x_grid = make_grid(generated_x, nrow=8).cpu().numpy()
# make data range to 0~1
generated_x_grid = (generated_x_grid * 0.5) + 0.5
plt.figure(figsize=(8, 8))
plt.title("Generated batch")
plt.imshow(np.transpose(generated_x_grid, (1, 2, 0)))
